Divisor Drips and Square Root Waves
by
Jeffrey Ventrella
Prime Numbers are the Holes in Complex Composite Number Patterns
free: Archive

buy: Amazon


1. A Pattern-Finding Journey
"Prime numbers are what is left when you have taken all the patterns away."
- Mark Haddon,
The Curious Incident of the Dog in the Night-Time ,
page 12
Write the numbers one through ten.

Four of those numbers are
prime
: 2, 3, 5, and 7. They have no integer divisors other than 1
and themselves. Now, write the integer divisors of these ten numbers in columns underneath,
spaced out vertically according to their sizes, as shown here.

As you would expect, there are visual gaps below the primes.
The other numbers have more divisors than 2.
They partially fill the right-triangular area below the row of 1's,
and above the diagonal string of numbers at the bottom-left.
These are the
composite numbers
. And if you ask me, they are
much more interesting than the primes!
You may not think this is a very interesting pattern.
But what if you keep extending the number line out really far, to a big number,
like, say, nine quintillion? Out there, you will witness some amazing stuff.
That stuff is what this book is about.
Once, when I was a young boy, I got a sheet of paper and a pencil, and started
plotting this graph, just for fun.

After plotting out the numbers up to a hundred,
I began to see patterns. At the time, I had never heard of the
Sieve of Eratosthenes,
but that is essentially what I was visualizing. Little did I know that twenty
years later I would gaze at the same graph of numbers - only this time on a
computer screen.
According to the mathematician Gregory Chaitin, "A concept is only as good as the
theorems that it leads to! ... instead of primes, perhaps we should be concerned with
the opposite, with the maximally divisible numbers!" [1]. I read this statement
in Chaitin's book
MetaMath!,
several decades after making that pencil drawing.
It got me remembering those patterns and the curiosity it provoked.
Having only gotten as far as the introduction of the book, I dropped it and
ran to my computer. It may have been Chaitin's excessive use of exclamation
marks that got me charged up, but I suspect it was something more!!!
I decided to return to this drawing and explore it in more depth. So I
created an interactive computer visualization
(which is now available at
divisorplot.com
It allows exploration of large numbers, with a greater range of divisors.
As I worked on the interactive tools to explore this space of numbers,
I found ever more patterns. I want to share with you some of the excitement
of these discoveries.
Let's scan a little farther out on the number line now. In the graph below, notice the patterns that start to emerge in the upper-right area.

If we zoom the view out even further and change the numerals to dots, we see even more patterns. Here are the divisors ranging from 1 to 120 for a section of the number line in the vicinity of 151,080.
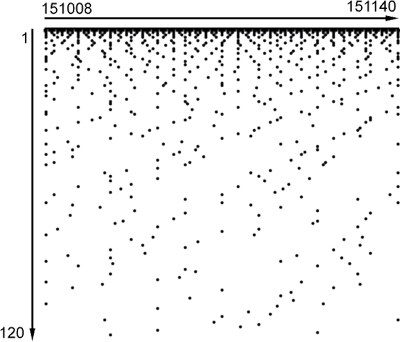
Why do these patterns appear complex, almost random? Especially considering the simplicity of the rule that is used to plot them. They exhibit apparent randomness, yes - but also some order. Fodder for the pattern-hungry human brain. That is really what this book is about - a quest to understand why these patterns exist.
This quest is explained from the standpoint of a non-mathematician: a visual language professional who, in the process of seeking out these patterns, becomes a mathematician, in the most universal and general sense - in the sense that all humans are mathematicians. It's just that most people speak a mathematical language of pictures, physical structures, gestures, music, and the rhythms of speech, rather than using a specialized alphabet of symbols connected together to make math notation.
While the creation of theorems and proofs may be the defining pinnacle of mathematics, the explorations that lead to them is universal to all humans. This very human kind of pattern-finding is what many educators believe we should encourage young students to experience: to internalize the beauty and value of mathematics, before having to read dense text books full of dry equations and disembodied formulas, devoid of purpose and stripped of aesthetics. Young or old, professional or novice, we are all pattern-finders.
Pattern-finding is the very creative, very human side of mathematics. In
The Music of the Primes,
Marcus du Sautoy explains how mathematicians often fluctuate between feeling that they are being creative and a sense that they are uncovering absolute truths. He says:
"Although the primes, and other aspects of mathematics, transcend cultural barriers, much of mathematics is creative and a product of the human psyche. Proofs, the stories mathematicians tell about their subject, can often be narrated in different ways. It is likely that Wiles's proof of Fermat's Last Theorem would be as mysterious to aliens as listening to Wagner's Ring cycle. Mathematics is a creative act under constraints - like writing poetry or playing the blues. Mathematicians are bound by the logical steps they must take in crafting their proofs. Yet within such constraints there is still a lot of freedom. Indeed, the beauty of creating under constraints is that you get pushed in new directions and find things you might never have expected to discover unaided. The primes are like notes in a scale, and each culture has chosen to play these notes in its own particular way, revealing more about historical and social influences than one might expect. The story of the primes is a social mirror as much as the discovery of timeless truths" [3].
Seeing things from different perspectives is what du Sautoy is talking about. But while he suggests that the prime numbers are "notes in a scale", and that each culture plays these notes in a different way, I believe that the primes are not like notes at all. They are the silent spaces between notes. The notes comprise a magnificent symphony, full of beautiful symmetry. And the instruments used to play that symphony are the composite numbers.
An important paradigm shift that this book follows is the idea that prime numbers are not the stars of the show. They are not the building blocks of all numbers. The stars of the show are the composite numbers, with symmetry and beautiful fractal-like structure that grows as you venture out along the number line to larger and larger numbers.
I hope that this book will make you think of "number" in a different way than it is typically described: not as a dry, boring symbol on a piece of paper, or as a concept that expresses a single quantity, but as a pattern situated inside a society of overlapping patterns with deep complex structure. If you listen closely to an extremely large composite number, you can hear a symphony playing inside. And that's not all: every number has it's own unique symphonic composition. And the primes? They don't make any sound.
Integer, Pattern, and Human Intelligence
While gazing at these divisor dots, rendered in white on a black background (as I prefer to render them on the computer screen), I have the sensation of being an ancient astronomer trying to find some order in the chaos. In the illustration below of a starry sky at dusk, it looks as if the stars are scattered randomly, but they are actually plotted out according to this very simple rule.

As you gaze at this Sky of Divisors, you may find Chariots, Big Bears, and Scorpions, as the ancient astronomers did. But for me, the most interesting patterns are the ones that reveal mathematical truths. Karl Sabbagh believes that if there is intelligent life elsewhere in the universe, it will be capable of numerical counting. "The stars in the sky are discrete points and cry out to be counted by intelligent beings throughout the universe (at least the ones who can see)." [8].
Counting naturally leads to truths such as 2+2=4, as well as all integer math, primes. etc. Leopold Kronecker said, "God created the integers; the rest is man's doing." We have magnificent occipital lobes, and our brains are wired to find patterns, at all levels - consciously and unconsciously. My exploration of these patterns begins with my visual pattern-seeking brain, and progressively applies language and math to my discoveries. I believe this is the natural trajectory of human mathematics.
Thinking Big
Rudy Rucker says,
"There are infinitely many natural numbers.
They surround us in all dimensions like an ocean without shores.
Compared to the ocean of number, our whole starry sky, all that is, is
less than a germ in the gut of a tube worm warming itself by a
volcanic vent at the bottom of the ten-kilometer-deep Marina Trench" [7].
Rucker uses colorful language to make a point: we are not able to grasp the vastness of really large numbers (such as ten to the power of one million).
But we can grasp patterns very well.
Small numbers are experienced quite easily, especially the very small numbers less than about 5, which are the
subitizable
ones (most of us can grasp them instantly in our minds without having to count: think of walking into a kitchen and noticing three apples in a bowl on the table). But as numbers get bigger, we need patterning, counting, iteration, to apprehend them. That's why we use the base ten (or any base) to clumpify numbers into scaling chunks. When numbers are really big, they can only be experienced as patterns.
As far as the brain is concerned, it may be that all numbers are processed as patterns (even the subitizable ones, except that our brains have special efficient neural networks that create what feels like instant recognition). Recent brain research has identified distinct patterns in the human parietal cortex associated with numerical processing for small numbers, and so we may soon find out more about this neural patterning.
 Ramanujan
Ramanujan
may have had abnormal neural networks allowing him to experience large primes with the same immediacy and instant clarity as a child apprehending three apples. Experiencing numbers really just comes down to patterns on the subconscious level (like everything else). But what really matters for communicating numbers are the languages we use to name them and the visualizations we use to understand them.
The larger the number, the harder it is for the human brain to grok it as a single quantity. And in fact, given the spectacular symmetry and interwoven internal structure found in the number 20! (twenty factorial), it is not very useful to think of it as a single quantity: 2,432,902,008,176,640,000. There is much more going on inside that number.
Overlapping Patterns
Based on the theories of Maxwell, Einstein, Schroedinger, de Broglie, Clifford, Wheeler,
Feynman, and many others, one might conclude that everything in the universe can be
described in terms of overlapping waves.
Ray Tomes
[12] suggests that the universe consists of many standing waves of many frequencies and overlapping in many ways. The combination of these waves produce harmonics.
Thomasson
[11],
Wolfram
[14], and others, have generated small variations of the graph I discovered to illustrate the distribution of primes. A few of these are shown here.

I presented my discoveries in October of 2007 at the
International Conference on Complex Systems
in Boston [13]. Since publishing the web site on divisorplot.com, many fellow prime number pattern explorers have contacted me, and some of their findings are shared in this book.
David Cox published similar findings in 2008, in a paper called
Visualizing the Sieve of Eratosthenes
[2]. An image reproduced from Cox's paper is shown below. We will address a few of Cox's observations later on.
 Building Blocks or Empty Spaces?
Building Blocks or Empty Spaces?
We hear of primes described as the "building blocks" of all numbers. Let's turn that concept on its head. Instead, let's think of primes as the negative spaces behind overlapping objects.
Imagine a series of picket fences stacked in front of each other. Each picket fence has different spacing between its wooden slats.
The superimposition of fences creates line
moire patterns.

Consider the
Sieve of Eratosthenes,
a process where each stage involves hopping along the number line with increasingly larger steps. This activity progressively stamps out the composite numbers, to identify primes. It's kind of like stacking these picket fences, each one with a larger gap between its slats - to eliminate the holes. Some holes will always remain. Those are the primes.
Asking the Wrong Questions
People are still asking, "What is the formula for the distribution of the primes on the number line?" "How can we predict when the next prime number will occur?" "What is the heartbeat of the primes?"
The heartbeat, by all accounts, has been fibrillating since the beginning of time, and its erratic behavior shows no sign of stopping. The problem is that these questions are based on a mental model that is stuck with marching along the number line from 0 to infinity. It is hyperlinear. The distribution of prime numbers might be better understood as the artifact of overlapping composite number patterns. For instance, take a look at this diagram of the first 100 primes against the graph of divisors.

I selected the composite numbers 42 and 60 as examples of how their immediate prime neighbors exhibit left-right symmetry. Actually, I have been told by a mathematician friend of mine that this symmetry is not just in the immediate neighborhood, but that it extends well beyond. And the reason that this symmetry appears to break down after a certain distance is because of the overlapping effect of many composite number patterns - each one having its own symmetrical pattern. Later on in the book we will explore more forms of symmetry about certain composite numbers.
A Definition
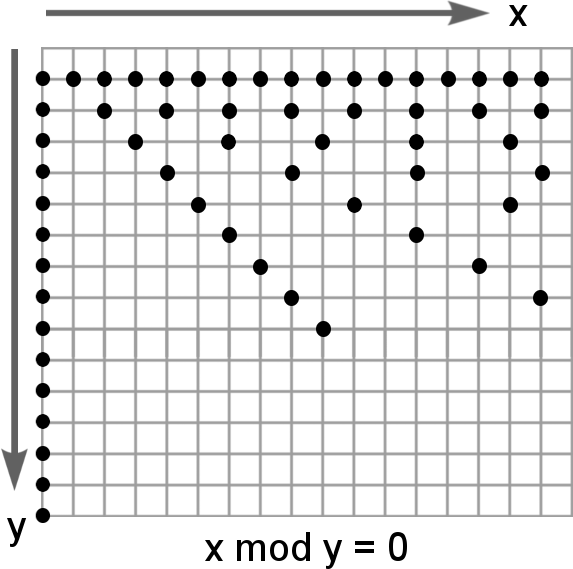
The graph I discovered when I was young doesn't appear to have a name, even though small versions of it have appeared at various times in the literature. I call this graph the "divisor plot". It can be defined as the set of all integer locations in the x,y plane (where y is positive) for which x mod y = 0. Let us call these integer locations "divisors". As integer locations, these divisors lie on a 2D lattice with cells of size 1. The y coordinate of each location is a divisor of x. I prefer to make the y axis point downward, so that higher y values are lower. It could just as easily be plotted the opposite way, but I find this way to be easiest for visualization.
 Unfurling the Divisor Function
Unfurling the Divisor Function
The number of divisors of an integer x (called the
divisor function
) is denoted as d(x). In this book, I will refer to the actual set of the divisors of x as Dx. As an example, D6 = {1, 2, 3, 6}. Every Dx is unique - and that fact is related to the fundamental theorem of arithmetic, which states that every integer can be described as a unique product of prime numbers: no two integers have the same set of prime number divisors. Similarly, no two integers have the same Dx.
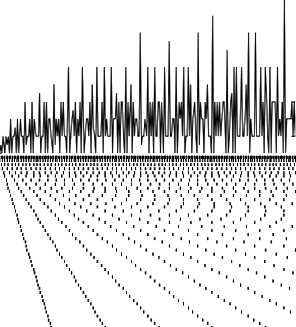
The divisor function is a counting of the number of divisors for an integer. If you plot a graph of the divisor function across the number line, you will notice that it is quite jaggy. This is directly related to the famously jaggy distribution of primes - the fibrillating heartbeat. Imagine compressing the divisor plot so that all the divisors get stacked up into vertical columns. The divisor function graph can be thought of as this vertical stacking of divisors in the divisor plot.
Sometimes, the way to understand something that is seemingly random is to see it as ground instead of figure, or as the shadow of something in a higher dimension. Perhaps that is how we should think of the prime numbers.


Numbers are typically considered as lying on a one-dimensional line. Think instead of the prime numbers as shadows cast by something in a higher dimension. Perhaps this is why Bernhard Riemann was able to discover
a new way to look at the primes:
he deployed the complex plane, a rich two-dimensional context within which to discover something about the distribution of primes [6].
Let's follow Chaitin's call to study the maximally-composite numbers instead of the primes.
Composites are the generators of all pattern. Prime numbers are the holes, the shadows,
the ground behind the figure. What passes through the Sieve of Eratosthenes is far
less interesting than the Sieve itself. Likewise, the tools we use to generate
random sequences such as the Golden Ratio and Pi (tools like the
Fibonacci sequence
and
Buffon's Needle
) are much more interesting than the random sequences themselves. After all, there is no information in random sequences. Why bother spending so much time looking at them?
Next chapter:
2. Divisor Drips and Reflection Rays

















